| Oracle® Database SQL Language Reference 11g Release 2 (11.2) Part Number E26088-03 |
|
|
PDF · Mobi · ePub |
| Oracle® Database SQL Language Reference 11g Release 2 (11.2) Part Number E26088-03 |
|
|
PDF · Mobi · ePub |
The linear regression functions are:
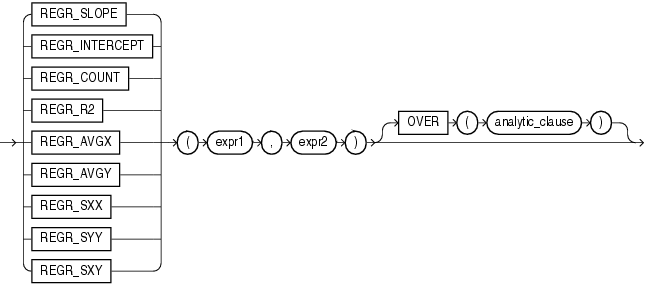
See Also:
"Analytic Functions" for information on syntax, semantics, and restrictionsThe linear regression functions fit an ordinary-least-squares regression line to a set of number pairs. You can use them as both aggregate and analytic functions.
These functions take as arguments any numeric data type or any nonnumeric data type that can be implicitly converted to a numeric data type. Oracle determines the argument with the highest numeric precedence, implicitly converts the remaining arguments to that data type, and returns that data type.
See Also:
Table 3-10, "Implicit Type Conversion Matrix" for more information on implicit conversion and "Numeric Precedence" for information on numeric precedenceOracle applies the function to the set of (expr1, expr2) pairs after eliminating all pairs for which either expr1 or expr2 is null. Oracle computes all the regression functions simultaneously during a single pass through the data.
expr1 is interpreted as a value of the dependent variable (a y value), and expr2 is interpreted as a value of the independent variable (an x value).
REGR_SLOPE returns the slope of the line. The return value is a numeric data type and can be null. After the elimination of null (expr1, expr2) pairs, it makes the following computation:
COVAR_POP(expr1, expr2) / VAR_POP(expr2)
REGR_INTERCEPT returns the y-intercept of the regression line. The return value is a numeric data type and can be null. After the elimination of null (expr1, expr2) pairs, it makes the following computation:
AVG(expr1) - REGR_SLOPE(expr1, expr2) * AVG(expr2)
REGR_COUNT returns an integer that is the number of non-null number pairs used to fit the regression line.
REGR_R2 returns the coefficient of determination (also called R-squared or goodness of fit) for the regression. The return value is a numeric data type and can be null. VAR_POP(expr1) and VAR_POP(expr2) are evaluated after the elimination of null pairs. The return values are:
NULL if VAR_POP(expr2) = 0
1 if VAR_POP(expr1) = 0 and
VAR_POP(expr2) != 0
POWER(CORR(expr1,expr),2) if VAR_POP(expr1) > 0 and
VAR_POP(expr2 != 0
All of the remaining regression functions return a numeric data type and can be null:
REGR_AVGX evaluates the average of the independent variable (expr2) of the regression line. It makes the following computation after the elimination of null (expr1, expr2) pairs:
AVG(expr2)
REGR_AVGY evaluates the average of the dependent variable (expr1) of the regression line. It makes the following computation after the elimination of null (expr1, expr2) pairs:
AVG(expr1)
REGR_SXY, REGR_SXX, REGR_SYY are auxiliary functions that are used to compute various diagnostic statistics.
REGR_SXX makes the following computation after the elimination of null (expr1, expr2) pairs:
REGR_COUNT(expr1, expr2) * VAR_POP(expr2)
REGR_SYY makes the following computation after the elimination of null (expr1, expr2) pairs:
REGR_COUNT(expr1, expr2) * VAR_POP(expr1)
REGR_SXY makes the following computation after the elimination of null (expr1, expr2) pairs:
REGR_COUNT(expr1, expr2) * COVAR_POP(expr1, expr2)
The following examples are based on the sample tables sh.sales and sh.products.
General Linear Regression Example
The following example provides a comparison of the various linear regression functions used in their analytic form. The analytic form of these functions can be useful when you want to use regression statistics for calculations such as finding the salary predicted for each employee by the model. The sections that follow on the individual linear regression functions contain examples of the aggregate form of these functions.
SELECT job_id, employee_id ID, salary, REGR_SLOPE(SYSDATE-hire_date, salary) OVER (PARTITION BY job_id) slope, REGR_INTERCEPT(SYSDATE-hire_date, salary) OVER (PARTITION BY job_id) intcpt, REGR_R2(SYSDATE-hire_date, salary) OVER (PARTITION BY job_id) rsqr, REGR_COUNT(SYSDATE-hire_date, salary) OVER (PARTITION BY job_id) count, REGR_AVGX(SYSDATE-hire_date, salary) OVER (PARTITION BY job_id) avgx, REGR_AVGY(SYSDATE-hire_date, salary) OVER (PARTITION BY job_id) avgy FROM employees WHERE department_id in (50, 80) ORDER BY job_id, employee_id; JOB_ID ID SALARY SLOPE INTCPT RSQR COUNT AVGX AVGY ---------- ----- ---------- ----- --------- ----- ------ ---------- --------- SA_MAN 145 14000 .355 -1707.035 .832 5 12200.000 2626.589 SA_MAN 146 13500 .355 -1707.035 .832 5 12200.000 2626.589 SA_MAN 147 12000 .355 -1707.035 .832 5 12200.000 2626.589 SA_MAN 148 11000 .355 -1707.035 .832 5 12200.000 2626.589 SA_MAN 149 10500 .355 -1707.035 .832 5 12200.000 2626.589 SA_REP 150 10000 .257 404.763 .647 29 8396.552 2561.244 SA_REP 151 9500 .257 404.763 .647 29 8396.552 2561.244 SA_REP 152 9000 .257 404.763 .647 29 8396.552 2561.244 SA_REP 153 8000 .257 404.763 .647 29 8396.552 2561.244 SA_REP 154 7500 .257 404.763 .647 29 8396.552 2561.244 SA_REP 155 7000 .257 404.763 .647 29 8396.552 2561.244 SA_REP 156 10000 .257 404.763 .647 29 8396.552 2561.244 . . .
REGR_SLOPE and REGR_INTERCEPT Examples
The following example calculates the slope and regression of the linear regression model for time employed (SYSDATE - hire_date) and salary using the sample table hr.employees. Results are grouped by job_id.
SELECT job_id, REGR_SLOPE(SYSDATE-hire_date, salary) slope, REGR_INTERCEPT(SYSDATE-hire_date, salary) intercept FROM employees WHERE department_id in (50,80) GROUP BY job_id ORDER BY job_id; JOB_ID SLOPE INTERCEPT ---------- ----- ------------ SA_MAN .355 -1707.030762 SA_REP .257 404.767151 SH_CLERK .745 159.015293 ST_CLERK .904 134.409050 ST_MAN .479 -570.077291
The following example calculates the count of by job_id for time employed (SYSDATE - hire_date) and salary using the sample table hr.employees. Results are grouped by job_id.
SELECT job_id, REGR_COUNT(SYSDATE-hire_date, salary) count FROM employees WHERE department_id in (30, 50) GROUP BY job_id ORDER BY job_id, count; JOB_ID COUNT ---------- ---------- PU_CLERK 5 PU_MAN 1 SH_CLERK 20 ST_CLERK 20 ST_MAN 5
The following example calculates the coefficient of determination the linear regression of time employed (SYSDATE - hire_date) and salary using the sample table hr.employees:
SELECT job_id, REGR_R2(SYSDATE-hire_date, salary) Regr_R2 FROM employees WHERE department_id in (80, 50) GROUP by job_id ORDER BY job_id, Regr_R2; JOB_ID REGR_R2 ---------- ---------- SA_MAN .83244748 SA_REP .647007156 SH_CLERK .879799698 ST_CLERK .742808493 ST_MAN .69418508
REGR_AVGY and REGR_AVGX Examples
The following example calculates the average values for time employed (SYSDATE - hire_date) and salary using the sample table hr.employees. Results are grouped by job_id:
SELECT job_id, REGR_AVGY(SYSDATE-hire_date, salary) avgy, REGR_AVGX(SYSDATE-hire_date, salary) avgx FROM employees WHERE department_id in (30,50) GROUP BY job_id ORDER BY job_id, avgy, avgx; JOB_ID AVGY AVGX ---------- ---------- ---------- PU_CLERK 2950.3778 2780 PU_MAN 4026.5778 11000 SH_CLERK 2773.0778 3215 ST_CLERK 2872.7278 2785 ST_MAN 3140.1778 7280
REGR_SXY, REGR_SXX, and REGR_SYY Examples
The following example calculates three types of diagnostic statistics for the linear regression of time employed (SYSDATE - hire_date) and salary using the sample table hr.employees:
SELECT job_id, REGR_SXY(SYSDATE-hire_date, salary) regr_sxy, REGR_SXX(SYSDATE-hire_date, salary) regr_sxx, REGR_SYY(SYSDATE-hire_date, salary) regr_syy FROM employees WHERE department_id in (80, 50) GROUP BY job_id ORDER BY job_id; JOB_ID REGR_SXY REGR_SXX REGR_SYY ---------- ---------- ----------- ---------- SA_MAN 3303500 9300000.0 1409642 SA_REP 16819665.5 65489655.2 6676562.55 SH_CLERK 4248650 5705500.0 3596039 ST_CLERK 3531545 3905500.0 4299084.55 ST_MAN 2180460 4548000.0 1505915.2